Data analytics (a.k.a. Big Data) has emerged as a primary data processing activity for business, science, and online services that attempt to extract insight from quantities of observation data. Increasingly, such analytics center on statistical machine learning (ML), in which an algorithm determines model parameters that make a chosen statistical model best fit the training data. Once fit (trained), such models can expose relationships among data items (e.g., for grouping documents into topics), predict outcomes for new data items based on selected characteristics (e.g., for recommendation systems), correlate effects with causes (e.g., for genomic analyses of diseases), and so on.

Growth in data sizes and desired model precision generally dictates parallel execution of ML algorithms on clusters of servers. Naturally, parallel ML involves the same work distribution, synchronization and data consistency challenges as other parallel computations. The PDL big-learning group has attacked these challenges, creating and refining powerful new approaches for supporting large-scale ML on Big Data. This short article overviews an inter-related collection of our efforts in this space.

Iterative Convergent ML

Most modern ML approaches rely on iterative convergent algorithms, such as stochastic gradient descent (SGD), to determine model parameter values. These algorithms start with some guess at a solution (a set of parameter values) and refine this guess over a number of iterations over the training data, improving an explicit goodness-of-solution objective function until sufficient convergence or goodness has been reached. Generally speaking, parallel realizations of iterative ML partition training data among the worker threads (running on available cores of each server used) that each contribute to computing the derived parameter values.

Historically, the most common parallel execution model for iterative ML has been based on the Bulk Synchronous Parallel (BSP) model. In BSP, each thread executes a given amount of work on a private copy of shared state and barrier synchronizes with the others. Once all threads reach the barrier, updates are exchanged among threads, and a next amount of work is executed. Commonly, in iterative ML, one iteration over the training data is performed between each pair of barriers.

Early parallel ML implementations used direct message passing among threads for coordination and update exchanges, forcing the ML application writer to deal with all of the complexities of parallel computing. The rise of map-reduce-style data processing systems, like Hadoop and Spark, allowed simpler implementations but suffer significant performance problems for parallel ML due to strict limitations on state sharing and communication among threads.

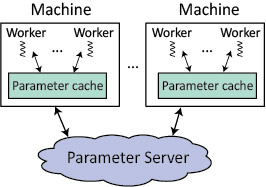
The most efficient modern frameworks for parallel ML use a parameter server architecture to make it easier for ML programmers to build and scale ML applications (“More Effective Distributed ML via a Stale Synchronous Parallel Parameter Server” [1], “Scaling Distributed Machine Learning with the Parameter Server” [2]). Figure 1 illustrates this architecture in which all state shared among worker threads is kept in a specialized key-value store, which is commonly sharded across the same machines used to execute the worker threads. Worker threads process their assigned training data using simple READ and UPDATE methods to check and adjust parameter values. UPDATE operations must be sufficiently commutative and associative that concurrent UPDATEs by different workers can be applied to the shared parameters in any order. To avoid constant remote communication, the client-side library caches parameter values locally and buffers updates.

Figure 1. Big-Learning Systems for ML on Big Data

Parameter Server Specialization

PDL has a strong track record of innovation on efficient, high-performance key-value store systems, such as FAWN, SILT, and MICA. Because a parameter server is a key-value store, much of PDL’s previous work applies. But, we have also found that unique characteristics of parallel ML invite specialization, such as to exploit the iterative-ness and convergence properties to increase efficiency and complete training more quickly.

Bounded Staleness. The convergence property allows a good solution to be found from any initial guess, as described above. This same property ensures that minor errors in the adjustments made by any given iteration will not prevent success. This imperfection tolerance can be exploited to improve performance by allowing parallel and distributed threads to use looser consistency models for shared state (i.e., the current solution). But, there must be limits to ensure success. We have developed new consistency models in which each thread works with a view of the current solution that may not reflect all updates from other threads. Allowing such staleness reduces communication costs (batched updates and cached reads) and synchronization (less waiting for locks or straggling threads). Our new flexible model, called Stale Synchronous Parallel (SSP), avoids barriers and allows threads to be a bounded number (the slack) of iterations ahead of the current slowest thread. The maximum amount of staleness allowed, dictated by a tunable slack parameter, controls a tradeoff between time-per-iteration and quality-per-iteration... the optimum value balances the two to minimize overall time to convergence. Both proofs and experiments demonstrate the effectiveness of SSP in safely improving convergence speed. For more information, see “Scaling Distributed Machine Learning with the Parameter Server” [1] and “Exploiting Bounded Staleness to Speed up Big Data Analytics” [3].

Exploiting Iterative-ness. The iterative-ness property creates an opportunity: knowable repeating patterns of access to the shared state (i.e., current parameter values). Often, each thread processes its portion of the training data in the same order in each iteration, and the same subset of parameters are read and updated any time a particular training data item is processed. So, each iteration involves the same pattern of reads and writes to the shared state. Our IterStore system demonstrates how the repeated patterns can be discovered efficiently and exploited to greatly improve efficiency, both within a multi-core machine and for communication across machines. Examples include replacing dynamic cache and server structures with static pre-serialized structures, informing prefetch and partitioning decisions, and determining which data should be cached at each thread to avoid both contention and slow accesses to memory banks attached to other sockets. We found that such specializations reduce per-iteration runtimes by 33-98%. For more information, see “Exploiting Iterative-ness for Parallel ML Computations” [4].

Managed Communication. Bounded staleness ensures a worst-case limit on the staleness observed by any worker, allowing convergence to be assured, but does not address the average staleness. Because staleness can result in imperfect parameter updates, which reduces quality-per-iteration and thereby requires more iterations, there is value in reducing it. For example, proactive propagation of updates reduces average staleness, but can reduce performance when network bandwidth is limited. Our Bösen system demonstrates how to maximize effective usage of a given network bandwidth budget. Through explicit bandwidth management, Bösen fully utilizes, but never exceeds, the identified bandwidth availability to communicate updates as aggressively as possible. Moreover, Bösen prioritizes use of limited bandwidth for messages that most affect algorithm convergence (e.g., those with the most significant updates). We found that such bandwidth management greatly improves convergence speeds and makes algorithm performance more robust to different cluster configurations and circumstances. For more information, see “Managed Communication and Consistency for Fast Data-Parallel Iterative Analytics” [5].

GPU Specialization. Large-scale deep learning, which is becoming increasingly popular for ML on visual and audio media, requires huge computational resources to train multi-layer neural networks. The computation involved can be done much more efficiently on GPUs than on traditional CPU cores, but training on a single GPU is too slow and training on distributed GPUs can be inefficient due to data movement overheads, GPU stalls, and limited GPU memory. Our GeePS system demonstrates specializations that allow a parameter server system to efficiently support parallel ML on distributed GPUs, overcoming these obstacles. For example, it uses pre-built indexes to enable parallel fetches and updates, GeePS-managed caching in GPU memory, and GPU-friendly background data staging. It also exploits iterative-ness observations and the layered nature of neural networks to stage data between GPU and CPU memories to allow training of very large models, overcoming GPU memory size limits. Experiments show excellent scaling across distributed GPUs. For more information, see “GeePS: Scalable Deep Learning on Distributed GPUs with a GPU-Specialized Parameter Server” [6].

Work Distribution and Scheduling

Most parallel ML implementations use a data-parallel approach. The training data is divided among worker threads that execute in parallel, each performing the work associated with their shard of the training data and communicating updates after completing each iteration over that shard. Typically, the assignment of work to workers stays the same from one iteration to the next. This continuity enables significant efficiency benefits, relative to independently scheduling work each iteration, in addition to avoiding potential scalability and latency challenges of a central scheduler. The efficiency benefits come from cache affinity effects (e.g., of the large training data) as well as from exploiting iterative-ness, yielding large benefits. But, we have developed ML-specific approaches to better distribute and schedule work among workers so as to adapt to dynamic cluster and ML algorithm behavior.

Straggler Mitigation. Parallel ML can suffer significant performance losses to stragglers. A straggler problem occurs when worker threads experience uncorrelated performance jitter. Each time synchronization is required, any one slowed worker thread can cause significant unproductive wait time for the others. Unfortunately, each if the load is balanced, transient slowdowns are common in real systems and have many causes, such as resource contention, garbage collection, background OS activities, and (for ML) stopping criteria calculations. Worse, the frequency of such issues rises significantly when executing on shared computing infrastructures rather than dedicated clusters and as the number of machines increases. Our FlexRR system demonstrates a solution to the straggler problem for iterative convergent ML. With temporary work reassignment, a slowed worker can offload a portion of its work for an iteration to workers that are currently faster, helping the slowed worker catch up. FlexRR’s specialized reassignment scheme complements bounded staleness, and both are needed to solve the straggler problem. Flexible consistency via bounded staleness provides FlexRR with the extra time needed to detect slowed workers and address them with temporary work reassignment, before any worker reaches the bound and is blocked. Experiments on Amazon EC2 and local clusters confirm FlexRR’s effectiveness. For more information, see “Solving the Straggler Problem for Iterative Convergent Parallel ML” [7].

Scheduled Model Parallelism. Although data-parallel implementations are the norm, an alternative and complementary strategy called model parallel is sometimes more effective. This strategy partitions model parameters for non-shared parallel access and updates, rather than having all threads access all parameters; so refinement of model parameters is partitioned among workers instead of the training data. Model parallelism can deal better with parameters that are dependent in ways that make concurrent adjustments induce too much error and with parameters that converge at very different rates. But, traditionally, model parallel implementations have been more complex to develop and less able to adapt to differing resource availability. Our STRADS system demonstrates a new approach, called scheduled model parallelism (SchMP), and shows that it can improve ML algorithm convergence speed by efficiently scheduling parameter updates, taking into account parameter dependencies and uneven convergence. For more information, see “STRADS: A Distributed Framework for Scheduled Model Parallel Machine Learning” [8].

References

[1] More Effective Distributed ML via a Stale Synchronous Parallel Parameter Server. Qirong Ho, James Cipar, Henggang Cui, Jin Kyu Kim, Seunghak Lee, Phillip B. Gibbons, Garth A. Gibson, Gregory R. Ganger, Eric P. Xing. NIPS ‘13, Dec. 2013, Lake Tahoe, NV.

[2] Scaling Distributed Machine Learning with the Parameter Server Mu Li, Dave Andersen, Alex Smola, Junwoo Park, Amr Ahmed, Vanja Josifovski, James Long, Eugene Shekita, Bor-Yiing Su. OSDI’14.

[3] Exploiting Bounded Staleness to Speed up Big Data Analytics. Henggang Cui, James Cipar, Qirong Ho, Jin Kyu Kim, Seunghak Lee, Abhimanu Kumar Jinliang Wei, Wei Dai, Gregory R. Ganger, Phillip B. Gibbons, Garth A. Gibson, Eric P. Xing. ATC’14, Philadelphia, PA.

[4] Exploiting Iterative-ness for Parallel ML Computations. Henggang Cui, Alexey Tumanov, Jinliang Wei, Lianghong Xu, Wei Dai, Jesse Haber-Kucharsky, Qirong Ho, Greg R. Ganger, Phil B. Gibbons, Garth A. Gibson, Eric P. Xing. SoCC’14, Seattle, WA, Nov. 2014.

[5] Managed Communication and Consistency for Fast Data-Parallel Iterative Analytics. Jinliang Wei, Wei Dai, Aurick Qiao, Qirong Ho, Henggang Cui, Gregory R. Ganger, Phillip B. Gibbons, Garth A. Gibson, Eric P. Xing. SoCC’15, Kohala Coast, HI.

[6] GeePS: Scalable Deep Learning on Distributed GPUs with a GPU-Specialized Parameter Server. Henggang Cui, Hao Zhang, Gregory R. Ganger, Phillip B. Gibbons, and Eric P. Xing. EuroSys’16, London, UK.

[7] Solving the Straggler Problem for Iterative Convergent Parallel ML. Aaron Harlap, Henggang Cui, Wei Dai, Jinliang Wei, Gregory R. Ganger, Phillip B. Gibbons, Garth A. Gibson, Eric P. Xing. Carnegie Mellon University Parallel Data Laboratory Technical Report CMU-PDL-15-102, April 2015.

[8] STRADS: A Distributed Framework for Scheduled Model Parallel Machine Learning. Jin Kyu Kim, Qirong Ho, Seunghak Lee, Xun Zheng, Wei Dai, Garth A. Gibson, Eric P. Xing. EuroSys’16, London, UK.