eScience: Site-City Effects in Large-scale 3D Earthquake Simulations
Ricardo Taborda, Julio López, Jacobo Bielak
Using Hercules—the octree-based finite-element earthquake simulator developed by the Quake group at Carnegie Mellon University—we have implemented new computational modules that allow us to incorporate large inventories of idealized buildings in earthquake simulations at scale, using parallel supercomputers. The buildings and their foundation systems are modeled as rectangular prismatic blocks filled with homogeneous material whose properties are set so that the fundamental dynamic properties of the real structures are matched on average. These models consist of the same solid finite-elements as those used for the crust and basin structure of the simulation domain and they are in full contact with the soil. We test our implementation with an inventory of 74 buildings placed near the edge of a realistic basin. Results indicate that the presence of the built environment greatly affects the area up to a perimeter of about 300 to 500 meters around the 'city' boundaries. Within the city, the ground motion exhibits significant changes in the spatial variability of peak response and reductions in the excitations at the base of the buildings. Synthetics exhibit shifts in both the time and the frequency domains. The structural response, in general, is reduced due to soil-structure interaction effects. This study suggests that larger inventories of buildings may have the potential of drastically changing the local and regional ground response and confirms results obtained in previous similar 2D studies.
Building Models and Meshing Process
We are interested in modeling large building inventories considering multiple, simultaneous and complete soil-foundation-structure systems fully incorporated in large-scale earthquake ground motion simulations, to study problems of site-city interaction effects and urban seismology.
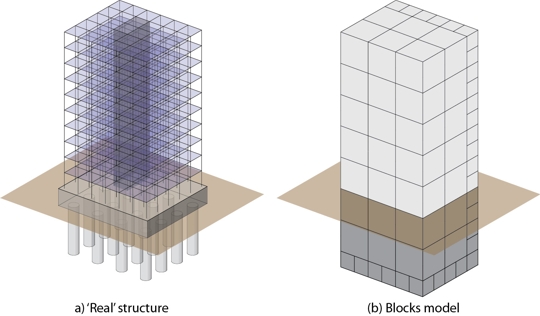
We model the foundation-structure systems using homogeneous blocks that are the same type of the solid hexahedral finite elements used for representing the crustal structure (Fig. 1). The material seismic velocities (Vs, Vp) used for the building elements are approximately derived from the dynamic characteristics of the buildings (fundamental period estimated from the height and number of stories) using (1) and (2), where hs is the interstory height. The density is estimated based on the building general properties. Typical values of Vs for the superstructure are about 100 m/s. Density is about 300 kg/m3.
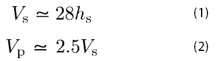
|
Figure 1. Building model using homogeneous blocks. The superstructure and foundation are replaced by hexahedral elements. Geometric characteristics are adjusted to the mesh. Properties of the superstructure and the foundation elements are independent of each other, and they reproduce the general dynamic characteristics of the real structure. |
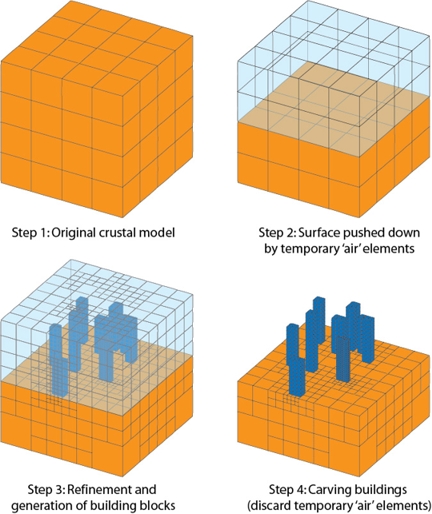
The building models are generated automatically at running time within Hercules meshing process, which was modified to adjust the simulation domain to include the urban setting as shown in Fig. 2.
|
Figure 2. Steps followed to generate building models during the meshing process without affecting the data-structure framework at the core of Hercules' end-to-end approach to large-scale earthquake ground motion simulation. Balancing of number of elements per processor occurs after removal of the temporary 'air' elements. |
Case Study
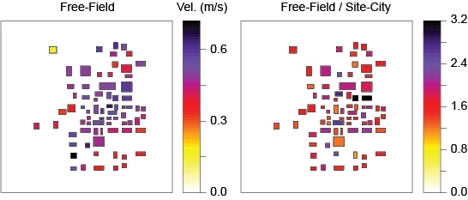
The Euroseistest Region and Earthquake Scenario
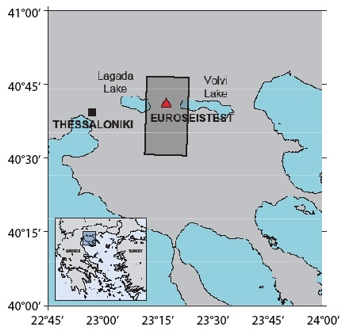
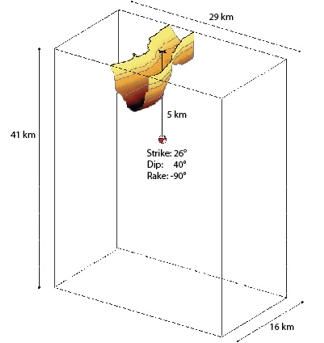
We build upon the model used for the Euroseistest Verification and Validation Project (Bard et al., 2008; Pitilakis, 2008). The simulation domain is a volume of 16 km x 29 km x 41 km that includes a portion of the Mygdonian basin between the Lagada and Volvi lakes near Thessaloniki, northern Greece (Fig. 3). The model of the basin is composed of three main deposits with Vs= 200, 350, and 650 m/s resting on a bedrock with Vs = 2600 m/s that increases with depth. We simulated an earthquake scenario of magnitude Mw 5.2, with hypocenter 5 km right beneath the valley (Fig. 4).
|
Figure 3. Region of interest and horizontal projection of the simulation domain. |
|
Figure 4. Simulation domain, and location and main characteristics of the source. |
Subregion of Interest and Buildings Inventory
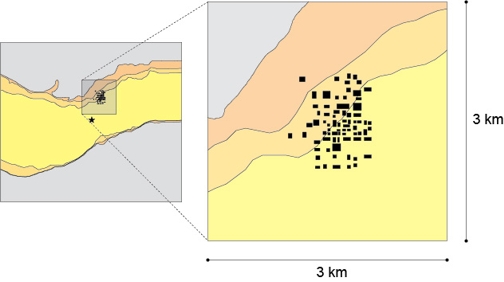
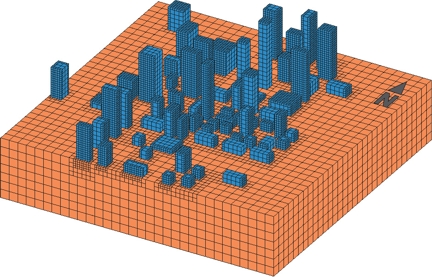
We focus on a subregion of 3 km x 3 km that encloses a hypothetical urban setting composed of 74 realistically arranged buildings with variable properties (Fig. 5). The buildings were artificially located near the North edge of the basin and Northwest from the epicenter. All building blocks have Vs= 100 m/s. The foundations have Vs= 400 m/s. Figure 6 shows a coarse representation of the mesh with the buildings. The minimum element size in a building is 2.5 m. The tallest building is 310 m. Fundamental periods vary between 0.4 and 7.3 s.
|
Figure 5. Location of the buildings inventory with reference to the central area of the simulation domain containing the basin. |
|
Figure 6. A coarse mesh representation of the 74 building models from the considered inventory. |
Simulation Parameters and Run Statistics
| Table 1. Simulation parameters | Table 2. Performance in Kraken at NICS. | ||||
| Maximum frequency Minimum Vs Domain size Simulation Δ t Simulation time Total time steps Min. size element Number of elements |
4 Hz 100 m/s 16 x 29 x 41 km3 0.001 s 20 s 20,000 2.5 m 71,798,354 |
Number of processors Total running time - Meshing time - Solving time - Core solver time - Balancing time - IO time Total service units (SU) |
8,290 s 1,173 s 6,935 s 5,357 s 1,355 s 256 s |
480 2:18:10 19:33 1:55:35 1:29:17 22:02 4:16 1,105 |
|
Results and Analysis
Peak Ground Response
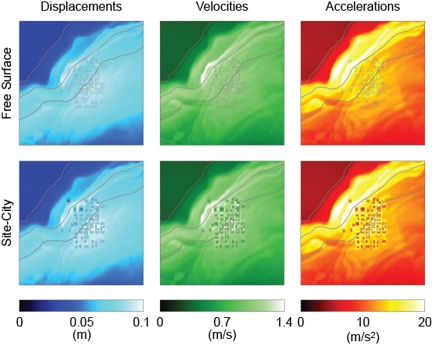
Figures 7 and 8 compare the surface ground response of the site-city case with that of the free-field (without buildings) for the subregion of interest. The effects due to the presence of the buildings are restricted to the area of the urban setting and a perimeter of about 300–500 m. In general, the magnitude of the ground motion beneath each building is attenuated because of the soil-foundation system, but it
is amplified in between buildings due to the multiple soil-structure interaction systems, channeling and scattering of waves. The changes (reductions and amplifications) introduced by the presence of the buildings significantly increases the spatial variability of the ground response within the city (Fig. 9).
|
Figure 7. Comparison of the surface horizontal peak magnitude displacement (left), velocity (center), and acceleration (right) for the simulations with (bottom) and without (top) considering the presence of the buildings. In the free-surface case the buildings are shown only for reference. |
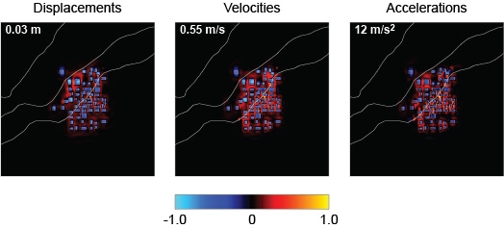
|
Figure 8. Normalized difference between the case with and without buildings for the surface horizontal peak magnitude of displacements (left), velocities (center), and accelerations (right). Warm colors indicate larger response in the site-city case, and cold colors otherwise. The absolute value of the maximum difference is shown in the top-left corner of each panel. |
|
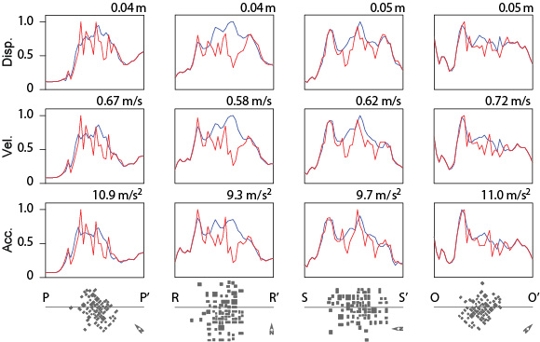
Figure 9. Comparison of peak displacements (top), velocities (middle), and accelerations (bottom), between the free-surface (blue) and site-city (red) cases in the EW component of motion along the four lines across the city. Each pair is normalized with respect to the largest of the two and the peak value is shown on the top-right corner of each panel. The horizontal projection of the city and the location of each line with respect to it is shown at the bottom. |
Base Excitation and Structural Response of the Buildings
We now consider the change in the excitation at the base of the buildings due to site-city interaction effects compared to the free field response at the same locations (Fig. 10); and the buildings response (at the roof) for the interaction problem compared to the response under fixed-base assumption, where the excitation is the motion recorded during the free-field simulation at the center of each building's base (Fig. 11). These results show that the structural response of the buildings is significantly attenuated because of soil-structure interaction effects that may be coupled with those of other buildings. Figures 12 and 13 summarize these effects for all buildings showing the response at the base and the roof for the free-field and fixed-base cases, and the reduction factors of the ratios with respect to the site-city interaction simulation. We observe reduction factors of up to 2.8 for the excitation peak velocities at the base, and up to 3.2 for the peak response at the roof of the buildings.
|
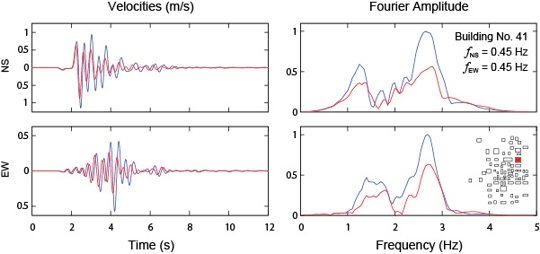
Figure 10. Comparison at the center of the base of a building between the cases with (red) and without (blue) the building models for the particle velocities in the two components of motion in both the time (left) and the frequency (right) domains. |
|
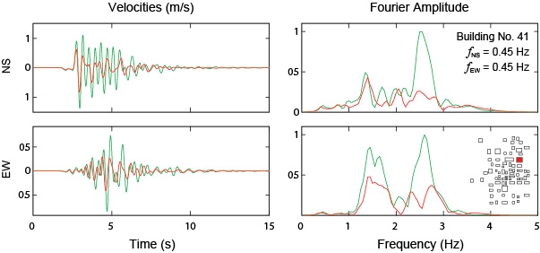
Figure 11. Comparison at the center of the roof of a buildings between the cases with (red) and without (green) soil-structure interaction for the particle velocities in the two components of motion in both the time (left) and the frequency (right) domains. |
|
Figure 12. Peak ground velocity at the location of the buildings for the free-field simulation (left), and reduction factor for the peak velocity of the excitation at the base of the buildings in the site-city case with respect to the free-field (right). |
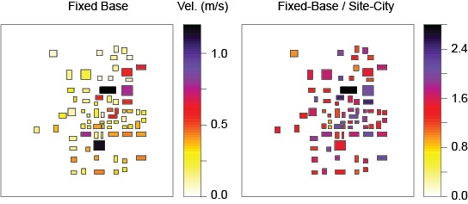
Figure 13. Peak response velocities at the roof of the buildings for the fixed-base (left) and reduction factor for the peak response at the roof of the buildings for the site-city interaction with respect to the fixed-base case (right). |
Conclusions
We have implemented a meshing procedure that allow us to incorporate large inventory of idealized building models in 3D earthquake ground motion simulations at scale to study site-city interaction effects and problems of urban seismology. Our results indicate that the presence of the built environment considerably changes the ground response and its spatial variability within and around the limits of the urban setting. In addition, soil-structure interaction systems cause a reduction in the structural response of buildings with foundations that have large impedance with respect to the soil.
REFERENCES
[1] Bard P.-Y., Chaljub E., Hollender F., Manakou M. and Pitilakis K. (2008), "Euroseistest Numerical Benchmark: Phase I", Commissariat à l'énergie atomique (CEC), Report distributed to the participants of the Cashima-Euroseistest Benchmark.
[2] Pitilakis K. (2008), "EuroSeisTest report for the Cashima project", Technical report, Department of Civil Engineering, Aristotle University of Thessaloniki, Greece, Report distributed to the participants of the Cashima-Euroseistest Benchmark.
People
LEAD RESEARCHER
Ricardo Taborda (post-doc CEE CMU)
FACULTY
Jacobo Bielak (CEE CMU)
Julio López
GRAD STUDENTS
Acknowledgements
This research is funded in part by the Southern California Earthquake Center (SCEC) through the NSF Cooperative Agreement EAR-0106924 and USGS Cooperative Agreement 02HQAG0008, in part by NSF-OCI award Towards Petascale Simulation of Urban Earthquake Impacts (NSF OCI-0749227), by the Gordon and Betty Moore Foundation in the eScience project, and an allocation through the TeraGrid Advanced Support Program. Computations were done using Kraken at the National Institute for Computational Sciences.
We thank the members and companies of the PDL Consortium: Amazon, Bloomberg LP, Datadog, Google, Honda, Intel Corporation, Jane Street, LayerZero Research, Meta, Microsoft Research, Oracle Corporation, Oracle Cloud Infrastructure, Pure Storage, Salesforce, Samsung Semiconductor Inc., and Western Digital for their interest, insights, feedback, and support.